5 loģiskās mīklas, lai atrastu modeļus

Jautājuma zīmes vietā aplī jābūt skaitlim 253. Šis ir princips, pēc kura tiek veidoti skaitļi apļos: katrs iepriekšējais tiek reizināts ar 2, un rezultātam tiek pievienots 3.

1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.

Vai arī šeit ir vēl viens risinājums: katram iepriekšējam skaitlim n-tajai jaudai pievieno 2.

1 + 2² = 1 + 4 = 5.
5 + 2³ = 5 + 8 = 13.
13 + 2⁴ = 13 + 16 = 29.
29 + 2⁵ = 29 + 32 = 61.
61 + 2⁶ = 61 + 64 = 125.
125 + 2⁷ = 125 + 128 = 253.

Jautājuma zīmes vietā kvadrātā jābūt burtam "P". Katra kvadrāta skaitļu summa ir burta kārtas numurs alfabētā. Pārbaudīsim:

6 + 4 + 4 = 14. "M" ir četrpadsmitais burts alfabētā. Mēs arī skaitām "Yo"!
4 + 1 + 7 = 12. "K" ir divpadsmitais burts alfabētā.
5 + 6 + 10 = 21. "U" ir divdesmit pirmais burts alfabētā.
1 + 14 + 2 = 17. "P" ir septiņpadsmitais burts alfabētā, kuram jābūt jautājuma zīmes vietā.

Jautājuma zīmes vietā jābūt skaitlim 179. Ja pārvietojaties pulksteņrādītāja kustības virzienā, sākot no 3, tad katrs nākamais skaitlis ir vienāds ar divkāršo iepriekšējo, kam pievienoti 1, 3, 5, 7, 9.

3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.

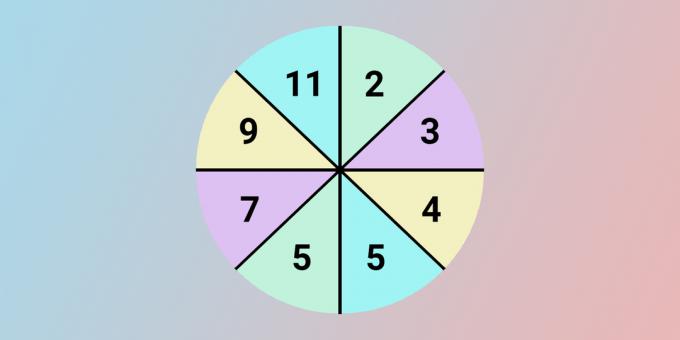
Jautājuma zīmes vietā jābūt skaitlim 11. Lai iegūtu katru skaitli no apļa kreisās puses, mēs ņemam skaitli no pretējā sektora, dubultojam un pievienojam vienu.

5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.

Jautājuma zīmes vietā skaitlim jābūt 66. Ja pārvietojaties pulksteņrādītāja kustības virzienā, sākot no 4, katrs nākamais skaitlis ir divreiz lielāks par iepriekšējo, no kura tika atņemti divi.

4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.